cross_corr_ar

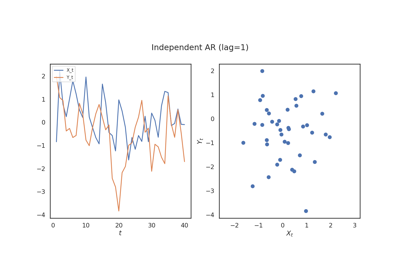
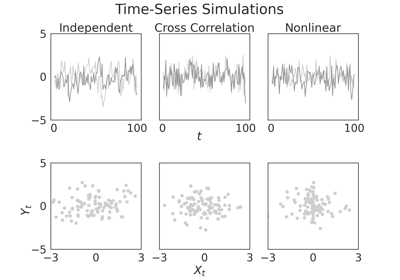
hyppo.tools.cross_corr_ar(n, lag=1, phi=0.5, sigma=1)

2 linearly dependent time series simulation.

\(X_t\) and \(Y_t\) are together a bivariate univarite AR(1ag) with \(\phi = \begin{bmatrix} 0 & 0.5 \\ 0.5 & 0 \end{bmatrix}\) for both series. Noise follows \(\mathcal{N}(0, \sigma)\). With lag (1), this is

\[\begin{split}\begin{bmatrix} X_t \\ Y_t \end{bmatrix} = \begin{bmatrix} 0 & \phi \\ \phi & 0 \end{bmatrix} \begin{bmatrix} X_{t - 1} \\ Y_{t - 1} \end{bmatrix} + \begin{bmatrix} \epsilon_t \\ \eta_t \end{bmatrix}\end{split}\]

Parameters

• n (int) -- The number of samples desired by the simulation (>= 3).

• lag (float, default: 1) -- The maximum time lag considered between x and y.

• phi (float, default: 0.5) -- The AR coefficient.

• sigma (float, default: 1) -- The variance of the noise.

Returns

x,y (ndarray of float) -- Simulated data matrices. x and y have shape (n,) where n is the number of samples.

Examples using hyppo.tools.cross_corr_ar

Time Series Testing

Time-Series Sims

previous

indep_ar

next

nonlinear_process